|
4 Collision Avoidance
| contents:
4.1 Alertness
4.2 Bike Handling 4.3 Avoiding Obstructions 4.4 Bicycle Lanes 4.5 Near Misses 4.6 Technical Details |
Summary: The following provides some hints on how to avoid collisions in incidents that result from an error on the part of cyclists or motorists, including what to watch out for, bike handling techniques, being predictable, avoiding obstructions, and what to so a near-miss occurs instead of an accident. There are a number of diagrams and most are drawn roughly to scale. The paths shown are based on calculations using elementary kinematics. A description of the mathematics is available in postscript form for interested parties.
Note: It is not possible to cover every possible situation that may occur. The following describes some situations that may occur, but is no an exhaustive treatment of every condition that a cyclist may face.
4.1 Alertness
Being aware of what others are doing may allow you to adjust to conditions before the situation requires some type of emergency maneuver.
 |
|
4.2 Bike Handling
The bike-handling skills relevant for collision avoidance basically are those that improve braking and turning. With good technique, you can achieve a deceleration of about 0.57g (where g is the acceleration due to gravity). Faster braking is possible, but with an increased risk of going over the handlebars in an uncontrolled fall. Similar accelerations are possible while turning. An acceleration of 0.57g corresponds to a turn in which the bicycle leans by 30 degrees from vertical.
4.2.1 Braking
The following figure illustrates the basic principles:
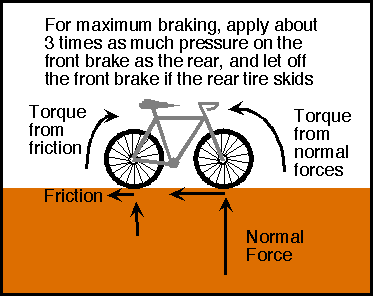
As your deceleration increases, the frictional forces create a torque that tends to flip the rider over handlebars. This torque is balanced by a torque resulting from normal forces (the force on the bike perpendicular to the ground). During braking, the normal forces shift forwards so that the normal force on the front tire is higher that on the rear. Once the normal force on the rear tire drops to zero, the bicycle is just at the point where the rider is about to flip over the handlebars. To stop efficiently,
- apply enough force on the rear brake for a gentle stop.
- increase the force on the front brake until the rear tire starts to skid. Once it does, reduce the pressure on the front brake, modulating it so that the rear tire is just on the verge of skidding.
The technique works because the slight pressure on the rear brake causes the rear tire to skid before the normal force on the rear tire drops to dangerously low levels (remember that you will flip over the handlebars when the normal force reaches zero). Keeping close to the point where the rear tire skids allows a sufficient safety margin, while still providing effective braking. By contrast, if you simply apply equal pressure on both the front and rear brakes, the rear tire will skid when the bicycle's deceleration is significantly lower.
If it has been raining and the rims are wet, the brakes will not work well until the wheel has rotated several times, forcing water out from under the pads as pressure is applied. Initially, you will have to apply equal pressure on both the front and rear brakes to "dry" them, and then you can brake as described above. The number of rotations needed to dry the brakes depends on the type of rims. Steel rims require more rotations than alloy rims. In wet weather, you may want to periodically apply the brakes to dry them, particularly if traffic conditions are such that you may have to make an unexpected stop.
Limitations:
- Gravel, oil or leaves on the road, wet pavement, or other conditions require lower levels of braking.
- You cannot brake hard and turn at the same time. While it is possible to brake while turning, if you brake too hard, the bike will skid out from under the cyclist, and there is no way of accurately determining your safety margin. Most cyclist brake before turns rather than during turns as a result.
- Under more difficult conditions (steep hills, perhaps with curves), the pressure on the front and rear brakes should be roughly equal, with due car exercised.
Warning: This technique is best learned from a trained instructor, and there is a chance of a fall while practicing it. If learning on your own, it is prudent to increase the level of braking slowly and only after you feel comfortable at lower levels.
4.2.2 Turning
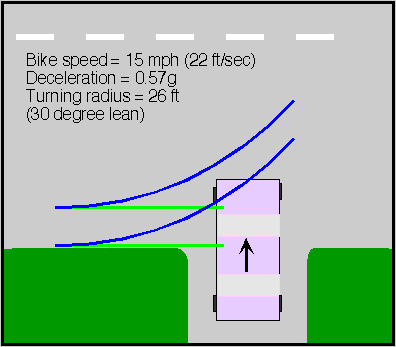
The radius of a turn is proportional to the square of your speed and inversely proportional to your acceleration (which in a turn is perpendicular to your direction of motion). You can initiate a turn quickly by twisting the handlebars temporarily in the direction opposite to your turn. For a right turn, you would thus turn the handlebars to the left for a split second and then straighten them out. The result is to move the bicycle a short distance to the left of the cyclist, causing the bicycle to lean to the right. As with braking, some practice is required. The following graph shows how increasing the angle at which the bike leans will decrease the turning radius.
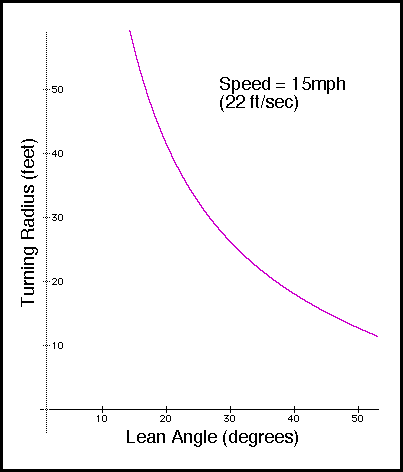
At an angle of 30 degrees from vertical, the turning radius is about 26.2 feet at 15 mph. Furthermore, as can be seen in the figure, a bit of practice (allowing the bicycle to lean further to the side) can make a big difference in tightening a turn.
4.2.3 Initiating Turns Early
You may, under some conditions, need to turn to avoid a car at a cross street (e.g., a car running a red light). The further you are from the curb, the sooner you can turn. By contrast, a bicycle right next to the curb cannot start a turn until the bicycle reaches the intersection, so such cyclists' only option is to brake. The following figure illustrates this.
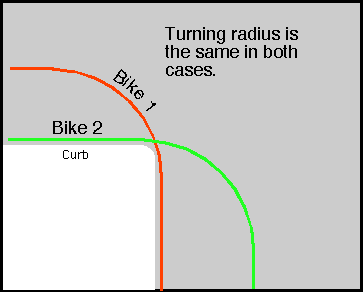
4.3 Avoiding Obstructions
Potholes and other obstacles are a fact of life. The trick to avoiding these safely is to arrange to be able to turn towards the curb to get around the obstruction rather than having to turn into the path of overtaking traffic. The following figure, illustrates how riding farther from the curb avoids the need to swerve in front of overtaking vehicles.
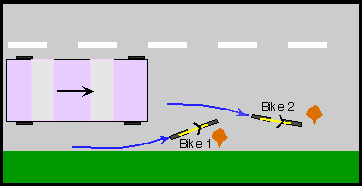
In this figure, the blue lines represent the path of a bicycle. The bicycle labeled Bike 1 can avoid a pothole only be swerving into the path of an overtaking vehicle because you cannot swerve to the right when you are already by the curb. Bike 2 can swerve to the right to avoid the pothole. In the figure, Bike 2 was initially in the path of the vehicle (which would have had ample time to see this bicycle), although with a wider lane, there would have been room for both to proceed side by side.
Parked cars are an additional hazard. Doors will open unexpectedly, and swerving to avoid an opening door may place you unexpectedly in the path of a motor vehicle. Swerving may not be possible at all, as is shown in the next figure.
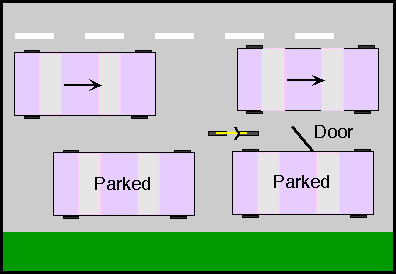
To avoid this situation, cyclists should ride far enough from parked cars that it is never necessary to swerve to avoid an opening door, as shown in the next figure.
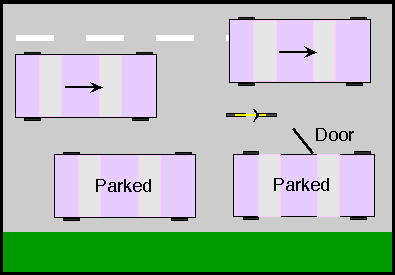
The figure shows how a cyclist can proceed in a straight line, regardless of whether or not a car door opens. An overtaking vehicle can pass by crossing partially into the next lane if necessary (waiting, of course, until such a lane change can be made safely).
Hint: Car doors will open unexpectedly, and it is not possible to see if someone is in a parked vehicle until it is to switch positions on the roadway or stop. The best policy is to leave enough clearance for the widest door that you may find: 3 feet or 1 meter of clearance is the bare minimum.
4.4 Bike Lanes
For the most part, bicycle lanes should be treated by cyclists the same as traffic lanes. Because cars are not generally allowed in bicycle lanes, however, you can ride in any part of the bicycle lane regardless of the speed of traffic. Nominally you should stay near the left edge to have as much clearance from parked cars and driveways as possible. If there is no debris in the bike lane, no parked cars or driveways, and you are not approaching an intersection, you may choose to ride closer to the curb. There are a few points that should be noted:
- Drivers often turn across bike lanes without first merging into the bike lanes. Essentially, these drivers treat the bike lane as a shoulder.
- Most drivers will use a bicycle lane when going straight (usually to get past a left-turning vehicle) and will on occasion cut off a cyclist in the bike lane
- Some bicycle lanes (usually older ones installed before the latest design standards were written) are too narrow for safety, with not enough clearance from parked cars, or are placed within right-turn-only lanes, or end by turning towards the curb. If a lane does not go where a cyclist is going, the lane should not be used, nor should it be used if staying in the bike lane puts the cyclist dangerously close to parked cars (whose doors can open at any time). In Section 21208, the California Vehicle Code grants permission to leave a bike lane, even when riding at a speed less than the normal speed of traffic, under these circumstances.
- Cyclists should look before moving sideways in a bicycle lane. Not only could a vehicle merge in unexpectedly, but another cyclist in the bicycle lane may be about to pass.
4.5 Near Misses
The following show some examples of situations of how to avoid collisions when someone makes a mistake. The first shows a situation in which a car enters the roadway and a bicycle is too close to stop. The green lines indicate the paths a bicycle would follow by just braking (the length denotes the stopping distance), and the blue lines indicate the paths a bicycle would follow by turning. Riding farther from the curb makes a significant difference in your ability to avoid a collision. The examples assume similar accelerations for stopping and turning. If the brakes are wet, but the pavement is free of mud or other debris, you may find that the acceleration is higher for turning than braking. Steep grades and windy roads also complicate the picture.
Unfortunately, you still have to be concerned about overtaking vehicles, and in such situations as the one shown above, there will not be sufficient time to look over your shoulder to see if a car is approaching from behind. Fortunately, most of the time, a car entering the roadway will creep forwards, trying not to get into the path of traffic until the driver can see clearly. An approaching cyclist is more likely to be noticed when riding where the motorist is looking, and the safety margin that the driver will nominally leave provides space for a cyclist to escape, as shown in the next figure (where the blue lines indicate a cyclist's path).
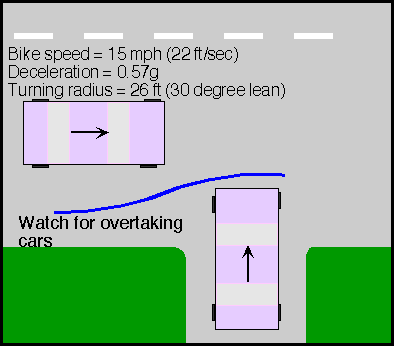
To follow this path, first turn left sharply and then straighten the bike out, arranging to pass a short distance in front of the vehicle which should be stopped. If the vehicle is stopped, assume that a car is approaching from behind you. If the vehicle entering the roadway continues to move, it is likely (but not certain) that no cars are behind you, so you may consider a sharp turn to avoid the car. Stopping if possible is, of course, a better option, but only if you have sufficient room.
The next figure shows the case in which a car crosses the path of a bicycle so that the bicycle, if it cannot stop in time, would hit the rear of the car. While serving would appear to help, in fact a bike that swerves arrives at the car's path sooner than a bike that stops. The earlier position of the car, at the time a turning bike would arrive, is shown in the following figure as a semitransparent image.
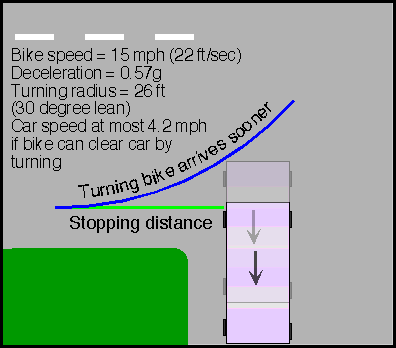
If the bike cannot clear the rear of the car by turning and in fact hits the car near its rear bumper, a bike continuing straight but braking will miss the car if the car speed is at least 4.2 mph. Curiously, if the accelerations for turning and braking are equal, and the bicycle has just enough room to stop as it reaches the car, then the minimum car speed is always equal to 0.2812 times the initial speed of the bicycle. The following graph shows, for a bicycle with an initial speed of 15 mph, what the minimum car speed is.
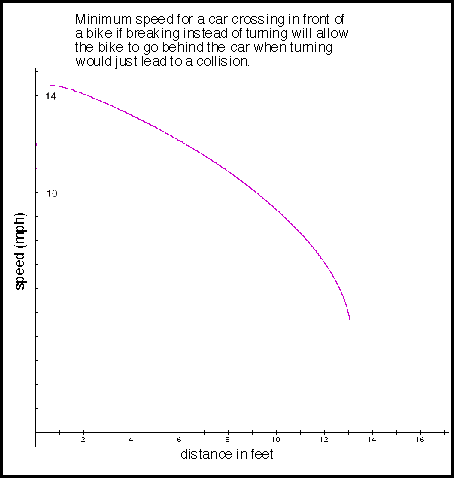
In this graph, the x axis is the distance between the bicycle and the path of the car when the bicycle starts to brake. As in the other examples, the bike speed is assumed to be initially 15 mph, with 0.57g deceleration for braking and 0.57g acceleration for turning (i.e., turning by leaning the bicycles 30 degrees from vertical). The x axis of the graph stops at about 13 feet because that is the distance needed for a bicycle to stop.
In some cases, braking may simply result in the bicycle stopping in front of the car. In this case, proceeding without braking may allow the bicycle to cross in front of the car without being hit because the bicycle arrives sooner without braking. Turning will result in the bicycle arriving a bit later than if it proceeded in a straight line. The bicycle will, however, cross further ahead of the car. This is shown in the next figure:
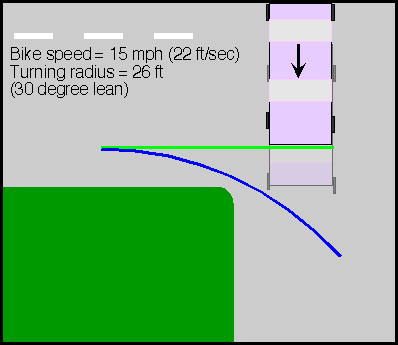
The partially transparent image of a car indicates the car's position when a bicycle is at the right end of the curved path, whereas the solid car indicates the car's position when the bicycle is at the right end of the straight path. The following graph shows the speed in mph above which a car that would just hit a bike proceeding straight (e.g., at the car's left front bumper) would also hit a bicycle that turned to avoid the collision.
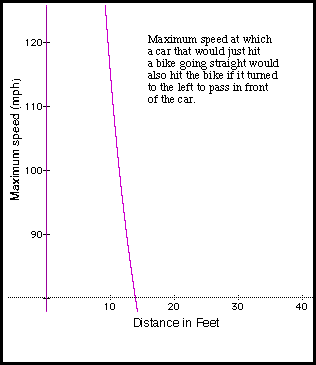
As should be obvious from the graph, turning when passing in front of a car heading from left to right perpendicular to your direction of travel is better than proceeding straight. In fact, regardless of the car's speed or the bike acceleration (assuming the acceleration when turning is equal in magnitude to the deceleration when braking), the maximum speed of the car for turning to be advantageous is 5.67 times the speed of the bicycle at the point where the bicycle would have stopped if it had braked instead. For a 15 mph bicycle (the case shown in the graph above), this speed is 85 mph.
Warning: These examples are based on particular assumptions about bicycle speed, and are somewhat idealized. They should be viewed as guidelines only for ideal cases.
4.6 Technical Details
A technical description in postscript showing the equations used to produce some of the graphs is available in a file named math.ps.
|